DFS 系列的第一节课
摘要
- 用分治法解决二叉树求值求路径的问题
- 理解什么是搜索中的回溯
- 用分治法解决二叉树形态变换的问题
- 全局变量在代码中的危害
分治法 Divide & Conquer
定义:将大规模问题拆分为若干个小规模的同类型问题去处理的算法
分治法和二分法 (Binary Search) 有什么区别?
- 二分法会每次丢弃掉一半留下一半
- 如二分查找 O (logN)
- 复杂度:T (n) = T (n/2) + O (x)
- 分治法分完以后两边都要处理
- 如归并排序
- 复杂度:T (n) = 2 T (n/2) + O (x)
什么样的数据结构适合分治法?
- 二叉树:整棵树的左子树和右子树都是二叉树
- 二叉树的大部分题都可以使用分治法解决
- 数组:一个大数组可以拆分为若干个不相交的子数组
- 归并排序,快速排序,都是基于数组的分治法
- 数组的题型还有其他的如:子数组、前缀和、双指针、滑动窗口等等
- 链表
独孤九剑 —— 破枪式
解决思路:碰到二叉树的问题,就想想整棵树在该问题上的结果和左右儿子在该问题上的结果之间的联系是什么
二叉树的高度是多少?
- 最坏 O (n)
- 最好 O (logN)
- 一般用 O (h) 来表示更合适
一棵二叉树有多少棵子树?
n 棵,每个节点都可以作为子树的根节点
二叉树考点剖析
- 第一类:Maximum / Minimum / Average / Sum / Paths
- 考察形态:二叉树上求值,求路径
- 代表例题:http://www.lintcode.com/problem/subtree-with-maximum-average/
- 考点本质:深度优先搜索 (Depth First Search)
- 第二类
- 考察形态:二叉树结构变化
- 代表例题:http://www.lintcode.com/problem/invert-binary-tree/
- 考点本质:深度优先搜索 (Depth First Search)
- 第三类
- 考察形态:二叉查找树 (Binary Search Tree)
- 代表例题:http://www.lintcode.com/problem/validate-binary-search-tree/
- 考点本质:深度优先搜索 (Depth First Search)
总结:Tree-based Depth First Search
- 不管二叉树的题型如何变化,考点都是基于树的深度优先搜索
一张图搞明白: 递归,DFS,回溯,遍历,分治,迭代
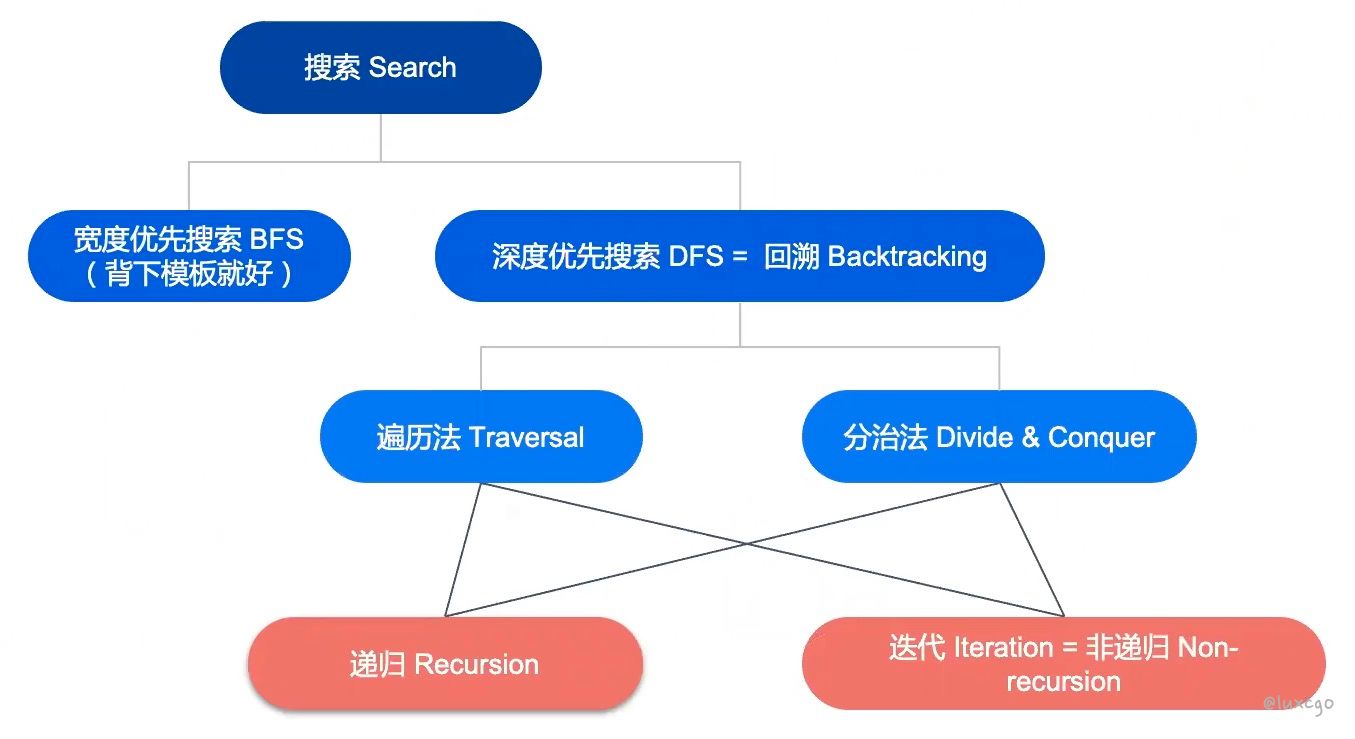
DFS 就是回溯,只是回溯包含显示的和隐式的。
将递归和非递归理解为算法的一种实现方式而不是算法
596 最小子树(第一类)
分治法
func FindSubtree2(root *TreeNode) *TreeNode {
_, subtree, _ := helper(root)
return subtree
}
func helper(root *TreeNode) (int, *TreeNode, int) {
if root == nil {
return math.MaxInt, nil, 0
}
leftMin, leftSubtree, leftWeight := helper(root.Left)
rightMin, rightSubtree, rightWeight := helper(root.Right)
rootWeight := leftWeight + rightWeight + root.Val
if leftMin < rightMin && leftMin < rootWeight {
return leftMin, leftSubtree, rootWeight
}
if rightMin < leftMin && rightMin < rootWeight {
return rightMin, rightSubtree, rootWeight
}
return rootWeight, root, rootWeight
}
474 最近公共祖先 II(第一类)
问法 1:如果有父指针
使用 HashSet 记录从 A 到根的所有点,访问从 B 到根的所有点,第一个出现在 HashSet 中的就是
func LowestCommonAncestorII(root, A, B *ParentTreeNode) *ParentTreeNode {
parentSet := map[*ParentTreeNode]bool{}
cur := A
for cur != nil {
parentSet[cur] = true
cur = cur.Parent
}
cur = B
for cur != nil {
if parentSet[cur] {
return cur
}
cur = cur.Parent
}
return nil
}
88 最近公共祖先(第一类)
问法 2:两个节点都在树里
给你 root, A, B 三个点的信息,A 和 B 保证都在 root 的下面
定义返回值:
- A, B 都存在 -> return LCA (A, B)
- 只有 A –> return A
- 只有 B –> return B
- A, B 都不存在 –> return nil
递归时间复杂度:递归一次 * 次数
递归空间复杂度:递归一次 + 递归深度
func LowestCommonAncestor(root, A, B *TreeNode) *TreeNode {
if root == nil {
return nil
}
// 如果root为A或B,立即返回,无需继续向下寻找
if root == A || root == B {
return root
}
// 分别去左右子树寻找A和B
left := LowestCommonAncestor(root.Left, A, B)
right := LowestCommonAncestor(root.Right, A, B)
// 如果A、B分别存于两棵子树,root为LCA,返回root
if left != nil && right != nil {
return root
}
// 左子树有一个点或者左子树有LCA
if left != nil {
return left
}
// 右子树有一个点或者右子树有LCA
if right != nil {
return right
}
// 左右子树啥都没有
return nil
}
578 最近公共祖先 III(第一类)
问法 3:两个节点不一定都在树里
root, p, q,但是不保证 root 里一定有 p 和 q
func LowestCommonAncestor3(root, A, B *TreeNode) *TreeNode {
a, b, lca := helper3(root, A, B)
if a && b {
return lca
}
return nil
}
func helper3(root, A, B *TreeNode) (bool, bool, *TreeNode) {
if root == nil {
return false, false, nil
}
leftA, leftB, leftNode := helper3(root.Left, A, B)
rightA, rightB, rightNode := helper3(root.Right, A, B)
a := leftA || rightA || root == A
b := leftB || rightB || root == B
if root == A || root == B {
return a, b, root
}
if leftNode != nil && rightNode != nil {
return a, b, root
}
if leftNode != nil {
return a, b, leftNode
}
if rightNode != nil {
return a, b, rightNode
}
return a, b, nil
}
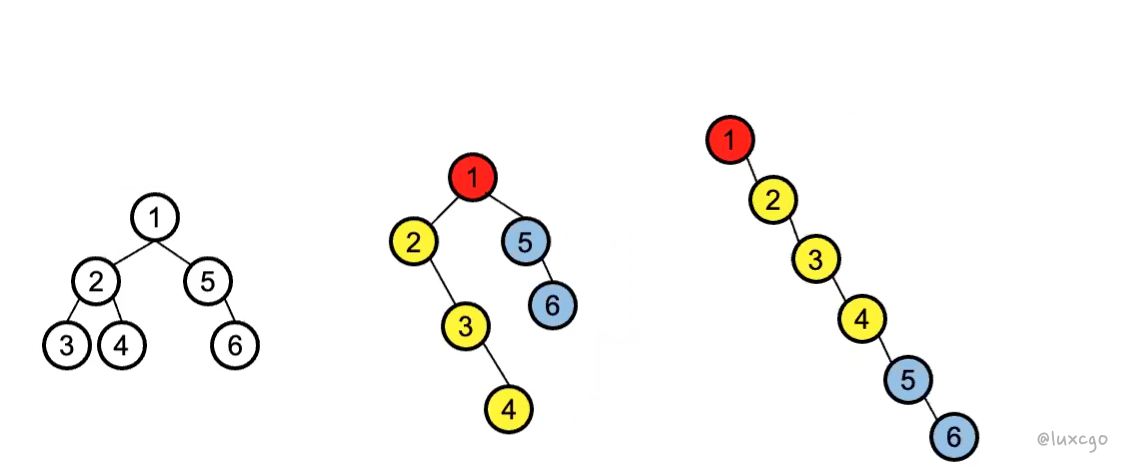
453 将二叉树拆成链表(第二类)
将二叉树拆成链表。进行前序遍历,将上一个节点的右指针指向当前节点。
func Flatten(root *TreeNode) {
flattenAndReturnLastNode(root)
}
func flattenAndReturnLastNode(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
leftLast := flattenAndReturnLastNode(root.Left)
rightLast := flattenAndReturnLastNode(root.Right)
if leftLast != nil {
leftLast.Right = root.Right
root.Right = root.Left
root.Left = nil
}
if rightLast != nil {
return rightLast
}
if leftLast != nil {
return leftLast
}
return root
}
二叉搜索树 | Binary Search Tree
BST 基本性质
-
从定义出发:
- 左子树都比根节点小 <
- 右子树都不小于根节点 ≥
-
从效果出发
- 中序遍历 in-order traversal 是“不下降”序列
-
性质:
-
如果一棵二叉树的中序遍历不是“不下降”序列,则一定不是 BST
-
如果一棵二叉树的中序遍历是不下降,也未必是 BST
- 比如下面这棵树就不是 BST,但是它的中序遍历是不下降序列。
- 要求是等于的情况只去一边,下面的不满足
1 / \ 1 1
-
-
高度:
- 同样是最坏 O (n) 最好 O (logn),用 O (h) 表示更合适
- 只有 Balanced Binary Tree (平衡二叉树) 才是 O (logn)
BST 基本操作
Build - 1359. Convert Sorted Array to Binary Search Tree
Insert - 85. Insert Node in a Binary Search Tree
Search - 1524. Search in a Binary Search Tree
Delete - 701. Trim a Binary Search Tree
Iterate - 86. Binary Search Tree Iterator
红黑树 | Red-black Tree
红黑树是一种 Balanced BST
- O (LogN) 的时间内实现增删查改
- O (LogN) 的时间内实现找最大找最小
- O (LogN) 的时间内实现找比某个数小的最大值 (upperBound) 和比某个数大的最小值 (lowerBound)
902 BST 中第 K 小的元素(第三类)
时间复杂度分析:O (k + h)
当 k 是 1 的时候 => O (h)
当 k 是 n 的时候 => O (n)
k 和 h 两者取大值
func KthSmallest(root *TreeNode, k int) int {
var stack []*TreeNode
for root != nil {
stack = append(stack, root)
root = root.Left
}
for i := 0; i < k-1; i++ {
node := stack[len(stack)-1]
if node.Right == nil {
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
for len(stack) != 0 && stack[len(stack)-1].Right == node {
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
}
} else {
node = node.Right
for node != nil {
stack = append(stack, node)
node = node.Left
}
}
}
return stack[len(stack)-1].Val
}
902 Follow up: 二叉树经常被修改
如何优化 kthSmallest 这个操作?
优化方法
在 TreeNode 中增加一个 counter,代表整个树的节点个数
也可以用一个 HashMap<TreeNode, Integer> 来存储某个节点为代表的子树的节点个数
在增删查改的过程中记录不断更新受影响节点的 counter
在 kthSmallest 的实现中用类似 Quick Select 的算法去找到 kth smallest element
时间复杂度为 O (h),h 为树的高度。
900 二叉搜索树中最接近的值(第三类)
递归
func ClosestValue(root *TreeNode, target float64) int {
if root == nil {
return 0
}
lowerNode := lowerBound(root, target)
upperNode := upperBound(root, target)
if lowerNode == nil {
return upperNode.Val
}
if upperNode == nil {
return lowerNode.Val
}
if target-float64(lowerNode.Val) > float64(upperNode.Val)-target {
return upperNode.Val
}
return lowerNode.Val
}
func lowerBound(root *TreeNode, target float64) *TreeNode {
if root == nil {
return nil
}
if target < float64(root.Val) {
return lowerBound(root.Left, target)
}
lowerNode := lowerBound(root.Right, target)
if lowerNode != nil {
return lowerNode
}
return root
}
func upperBound(root *TreeNode, target float64) *TreeNode {
if root == nil {
return nil
}
if target >= float64(root.Val) {
return upperBound(root.Right, target)
}
upperNode := upperBound(root.Left, target)
if upperNode != nil {
return upperNode
}
return root
}
非递归
func ClosestValue(root *TreeNode, target float64) int {
upper := root
lower := root
for root != nil {
if target < float64(root.Val) {
upper = root
root = root.Left
} else if target > float64(root.Val) {
lower = root
root = root.Right
} else {
return root.Val
}
}
if math.Abs(float64(upper.Val)-target) < math.Abs(float64(lower.Val)-target) {
return upper.Val
} else {
return lower.Val
}
}
901 二叉搜索树中最接近的值 II(第三类)
方法 1 暴力做法
- 先用 inorder traversal 求出中序遍历
- 找到第一个 >= target 的位置 index
- 从 index-1 和 index 出发,设置两根指针一左一右,获得最近的 k 个整数
方法 2 使用两个 Iterator
- 一个 iterator move forward
- 另一个 iterator move backward
- 每次 i++ 的时候根据 stack,挪动到 next node
- 每次 i– 的时候根据 stack,挪动到 prev node
func ClosestKValues(root *TreeNode, target float64, k int) []int {
if root == nil || k == 0 {
return nil
}
s := &sol{
lowerStack: getStack(root, target),
upperStack: getStack(root, target),
}
if target > float64(s.lowerStack[len(s.lowerStack)-1].Val) {
s.moveUpper()
} else {
s.moveLower()
}
var res []int
for i := 0; i < k; i++ {
if s.isLowerCloser(target) {
res = append(res, s.lowerStack[len(s.lowerStack)-1].Val)
s.moveLower()
} else {
res = append(res, s.upperStack[len(s.upperStack)-1].Val)
s.moveUpper()
}
}
return res
}
func getStack(root *TreeNode, target float64) []*TreeNode {
var stack []*TreeNode
for root != nil {
stack = append(stack, root)
if target < float64(root.Val) {
root = root.Left
} else {
root = root.Right
}
}
return stack
}
type sol struct {
lowerStack []*TreeNode
upperStack []*TreeNode
}
func (s *sol) moveUpper() {
node := s.upperStack[len(s.upperStack)-1]
if node.Right != nil {
node = node.Right
for node != nil {
s.upperStack = append(s.upperStack, node)
node = node.Left
}
} else {
s.upperStack = s.upperStack[:len(s.upperStack)-1]
for len(s.upperStack) > 0 && s.upperStack[len(s.upperStack)-1].Right == node {
node = s.upperStack[len(s.upperStack)-1]
s.upperStack = s.upperStack[:len(s.upperStack)-1]
}
}
}
func (s *sol) moveLower() {
node := s.lowerStack[len(s.lowerStack)-1]
if node.Left != nil {
node = node.Left
for node != nil {
s.lowerStack = append(s.lowerStack, node)
node = node.Right
}
} else {
s.lowerStack = s.lowerStack[:len(s.lowerStack)-1]
for len(s.lowerStack) > 0 && s.lowerStack[len(s.lowerStack)-1].Left == node {
node = s.lowerStack[len(s.lowerStack)-1]
s.lowerStack = s.lowerStack[:len(s.lowerStack)-1]
}
}
}
func (s *sol) isLowerCloser(target float64) bool {
if len(s.lowerStack) == 0 {
return false
}
if len(s.upperStack) == 0 {
return true
}
return target-float64(s.lowerStack[len(s.lowerStack)-1].Val) < float64(s.upperStack[len(s.upperStack)-1].Val)-target
}
Related Questions
- Search Range in Binary Search Tree
- Insert Node in a Binary Search Tree
- Remove Node in a Binary Search Tree
- http://www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/9-BinTree/BST-delete.html

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。