摘要
- 排列组合类搜索
- 两种组合类 DFS 的实现方法
- 使用组合类 DFS 算法解决 K 数之和问题
- DFS 的框架模板
- 矩阵上的 DFS
- 如何解决求所有最短路线的问题
DFS 深度优先搜索回顾
从一点开始,任选一条路走到下一个点,直到走到尽头
如果走到尽头,回撤一步,换条路继续走
在遍历的过程中搜索目标值或者目标路径
在同一条路径中不走重复点,在不同路径中走过的点可能可以重复走
BFS vs DFS 复杂度
时间复杂度均为:O (V+E),V 为顶点个数,E 为边个数
- 宽度优先搜索的空间复杂度取决于宽度
- 深度优先搜索的空间复杂度取决于深度
递归定义
一般来说,如果面试官不特别要求的话,DFS 都可以使用递归 (Recursion) 的方式来实现。
先递进,再回归——这就是「递归」 简单来说递归就是方法自己调用自己,每次调用时传入不同的变量。一直到程序执行到指定的出口时停止调用本身,并将结果层层返回。
Recursion (递归) 和 iteration (迭代) 都是代码的实现方式,并不是一种算法
递归三要素是实现递归的重要步骤:
- 递归的定义
- 递归的拆解
- 递归的出口
什么时候使用 DFS?
在之前的课程中,我们知道了二叉树 (Binary Tree) 的问题大部分都可以用 DFS 求解。除了二叉树以外的 90% DFS 的题,要么是组合 (combination),要么是排列 (permutation)。
碰到让你找所有方案的题,基本可以确定是 DFS
如果题目给了你一个树或者图,可以在上面进行 DFS
如果题目没有直接给你一个树或图,可以把题目的解空间看成一个树或图,然后在上面进行 DFS。找到树或图中的所有满足条件的路径。
路径 = 方案 = 图中节点的排列组合
独孤九剑 —— 破索式
碰到让你找所有方案的题,基本可以确定是 DFS
除了二叉树以外的 90% DFS 的题,要么是排列,要么是组合
组合 Combination
组合要点
[a, b, c]的所有组合为:
0个元素: []
1个元素: [a], [b], [c]
2个元素: [a, b], [a, c], [b, c]
3个元素: [a, b, c]
问题模型
求出所有满足条件的“组合”。
判断条件
组合中的元素是顺序无关的。
时间复杂度
与 2^n 相关 (比如,[a, b, c] 的所有组合有 2^3 = 8 种)
O (方案个数 * 构造每个方案的时间) = O (2^n * n)
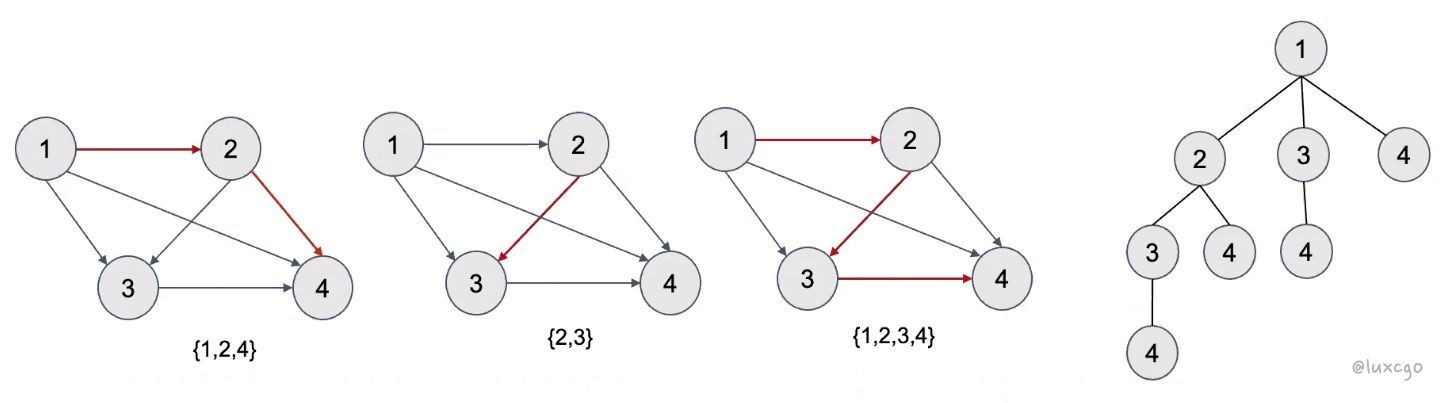
组合图解 (找出一个集合的所有子集)
点:集合中的元素
边:元素与元素之间用有向边连接,小的点指向大的点 (为了避免选出 12 和 21 这种重复集合)
路径 = 子集 = 图中任意点出发到任意点结束的一条路径
425 电话号码的字母组合
func LetterCombinations(digits string) []string {
paths := []string{}
if len(digits) == 0 {
return paths
}
dict := []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
dfs(dict, digits, 0, nil, &paths)
return paths
}
func dfs(dict []string, digits string, idx int, path []rune, paths *[]string) {
if idx == len(digits) {
*paths = append(*paths, string(path))
return
}
for _, letter := range dict[digits[idx]-'2'] {
path = append(path, letter)
dfs(dict, digits, idx+1, path, paths)
path = path[:len(path)-1]
}
}
90 k Sum II, k 数和 II
K 个元素的组合,和为 target,数字不可以重复用

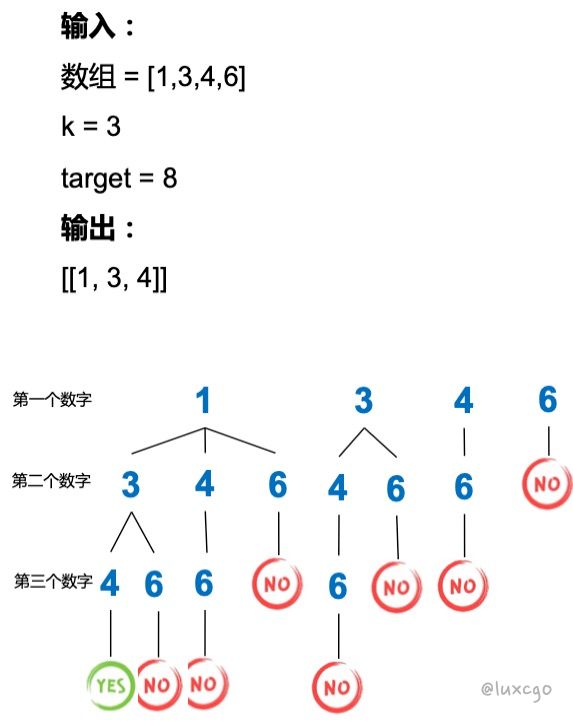
func KSumII(a []int, k int, target int) [][]int {
// 这里需要sort(a)吗?不需要,本题无需按照字母序,也无重复
// 排序所有字母,排序的意义:
// 1.可以按照字母序得到结果
// 2.相同的字母在一起,方便去重
subsets := [][]int{}
dfsKSumII(a, k, target, 0, nil, &subsets)
return subsets
}
func dfsKSumII(a []int, k int, target int, idx int, subset []int, subsets *[][]int) {
if k == 0 && target == 0 {
// log.Println(subset)
*subsets = append(*subsets, append([]int{}, subset...))
return
}
if k == 0 || target <= 0 {
return
}
for i := idx; i < len(a); i++ {
// log.Printf("i = %d, a[i] = %d, k = %d, target = %d, idx = %d", i, a[i], k, target, idx)
subset = append(subset, a[i])
dfsKSumII(a, k-1, target-a[i], i+1, subset, subsets)
subset = subset[:len(subset)-1]
}
}
135 数字组合

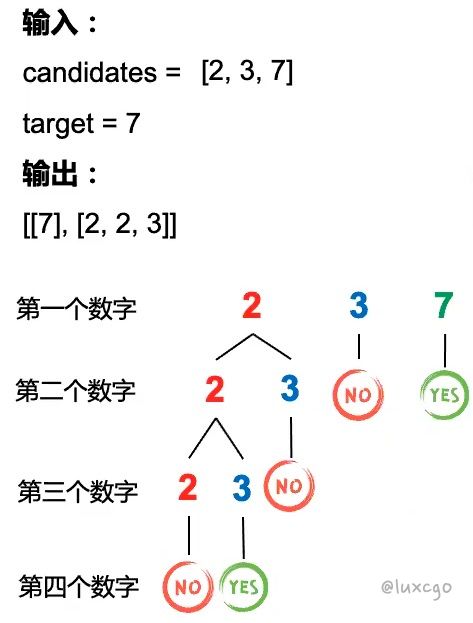
func CombinationSum(candidates []int, target int) [][]int {
subsets := [][]int{}
if len(candidates) == 0 {
return subsets
}
dict := removeDuplicatesAndSort(candidates)
dfsCombinationSum(dict, target, 0, nil, &subsets)
return subsets
}
func dfsCombinationSum(dict []int, target int, idx int, subset []int, subsets *[][]int) {
if target == 0 {
*subsets = append(*subsets, append([]int{}, subset...))
}
for i := idx; i < len(dict); i++ {
if target < dict[i] {
break
}
subset = append(subset, dict[i])
dfsCombinationSum(dict, target-dict[i], i, subset, subsets)
subset = subset[:len(subset)-1]
}
}
func removeDuplicatesAndSort(nums []int) []int {
n := len(nums)
if n == 0 {
return nums
}
sort.Ints(nums)
slow := 1
for fast := 1; fast < n; fast++ {
if nums[fast] != nums[fast-1] {
nums[slow] = nums[fast]
slow++
}
}
return nums[:slow]
}
排列 Permutation
排列要点
[a, b, c]的所有排列(全排列)为:[a, b, c], [a, c, b], [b, a, c] ], [b, c, a], [c, a, b], [c, b, a]
问题模型
求出所有满足条件的“排列”。
判断条件
组合中的元素是顺序“相关”的
时间复杂度
与 n! 相关 (比如,[a, b, c]的所有排列有 3! = 3*2*1 = 6种)
O (方案个数 * 构造每个方案的时间) = O (n! * n)
排列图解 (求出 N 个数组成的全排列)
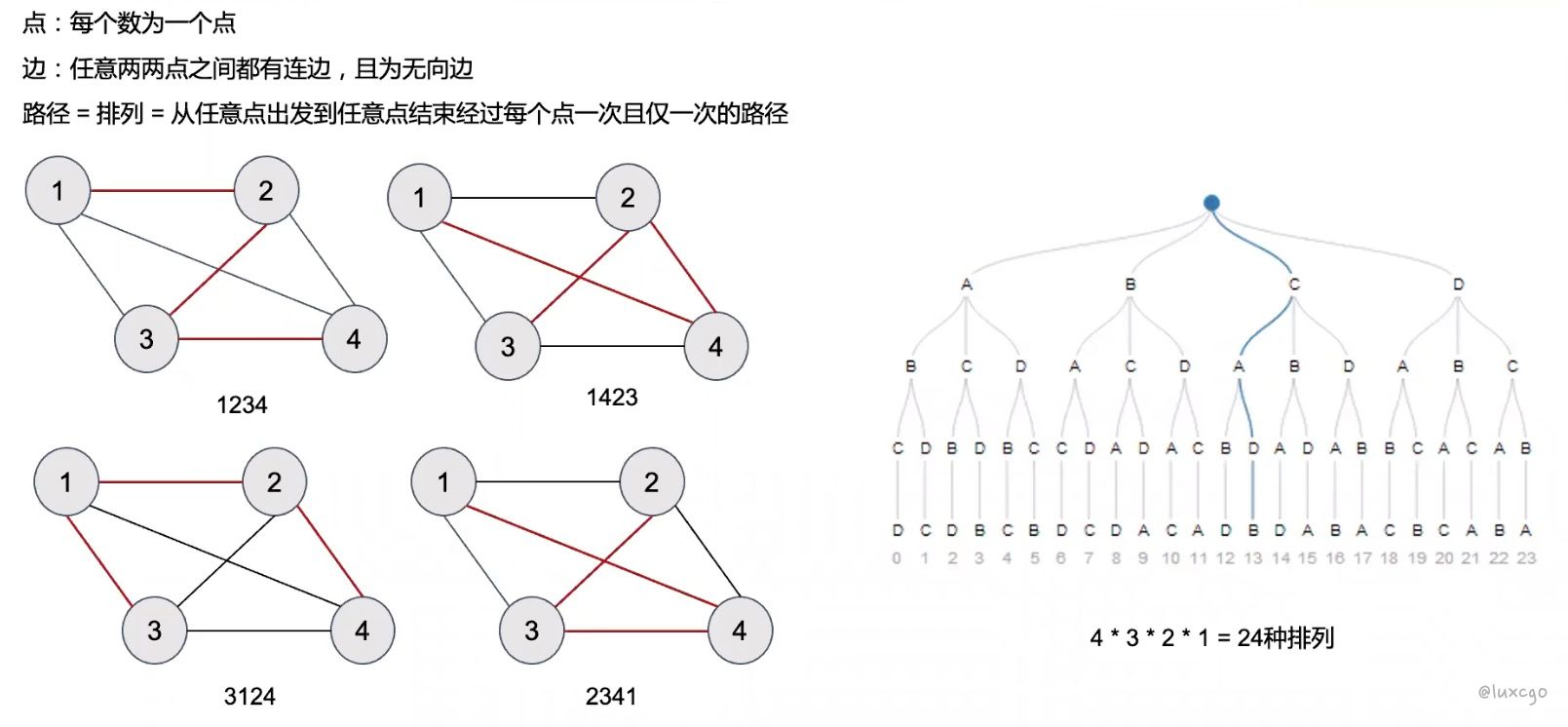
10 String Permutation II 字符串的不同排列

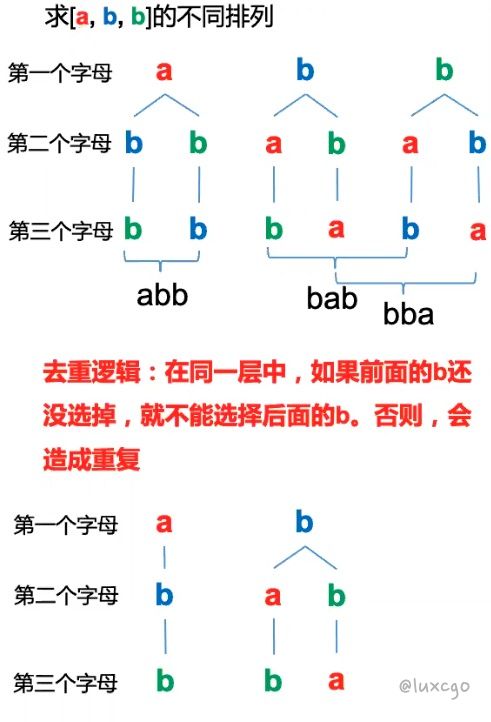
func StringPermutation(str string) []string {
permutations := []string{}
if str == "" {
return permutations
}
chars := []rune(str)
sort.Slice(chars, func(i, j int) bool {
return chars[i] < chars[j]
})
visited := make([]bool, len(chars))
stringPermutationDfs(chars, visited, []rune{}, &permutations)
return permutations
}
func stringPermutationDfs(chars []rune, visited []bool, permutation []rune, permutations *[]string) {
if len(permutation) == len(chars) {
*permutations = append(*permutations, string(permutation))
}
for i, char := range chars {
if visited[i] {
continue
}
if i > 0 && char == chars[i-1] && !visited[i-1] {
continue
}
visited[i] = true
permutation = append(permutation, char)
stringPermutationDfs(chars, visited, permutation, permutations)
permutation = permutation[:len(permutation)-1]
visited[i] = false
}
}
在已知的图或树上遍历
- 字母矩阵 (Character Matrix)
- 词语接龙 (Word Ladder)
BFS+DFS 题目解析
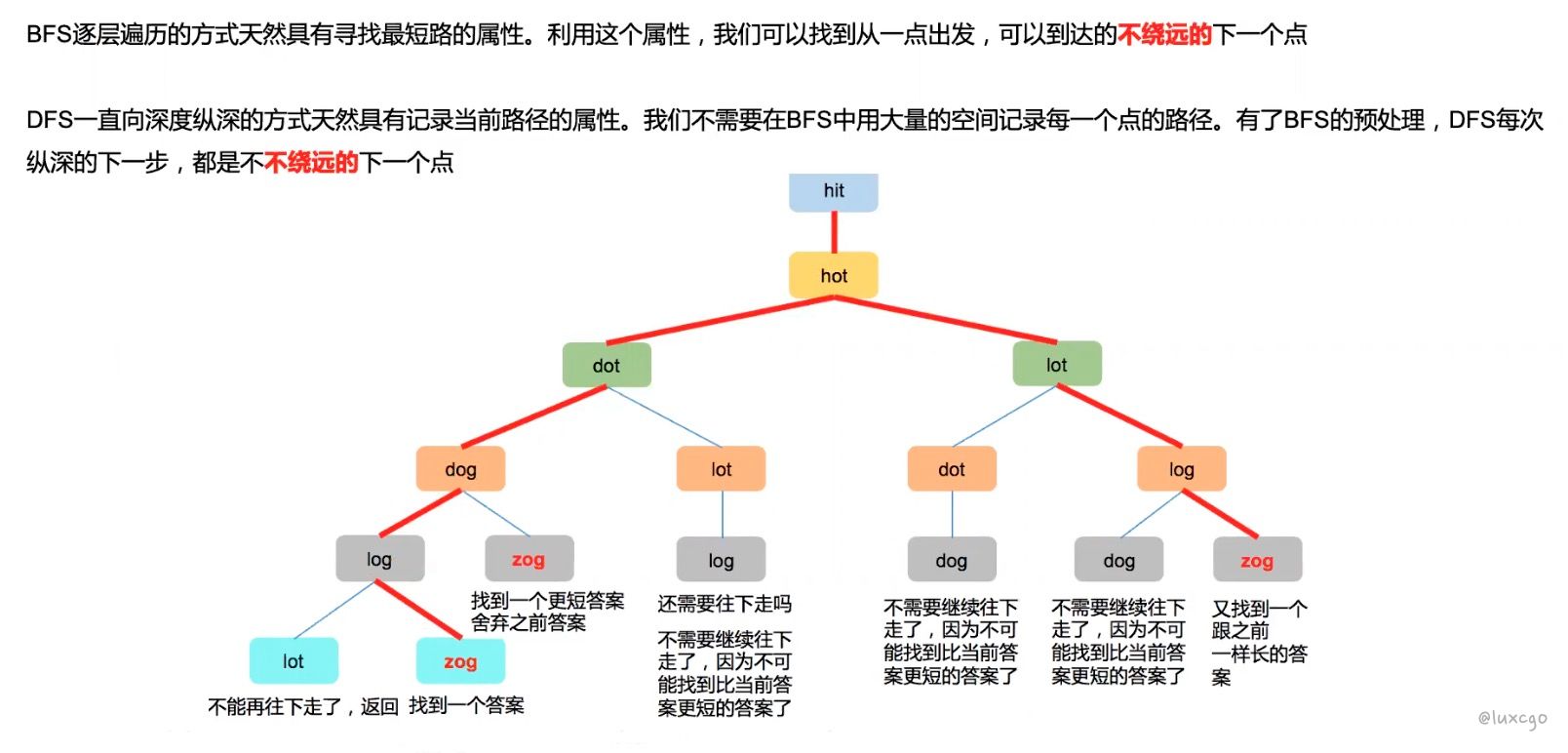
132 Word Search II 单词搜索 II
字母矩阵 (Character Matrix)
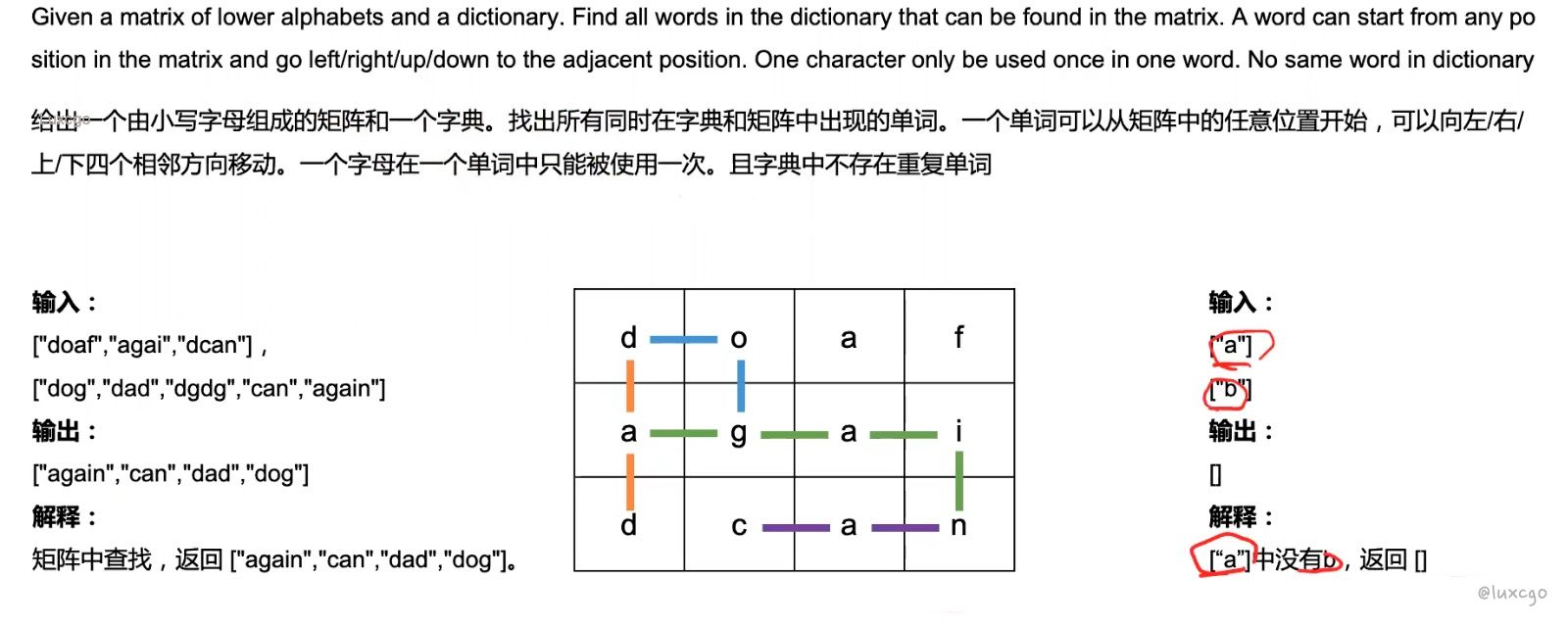
func WordSearchII(board [][]byte, words []string) []string {
var res []string
if len(board) == 0 || len(board[0]) == 0 {
return res
}
visited := make([][]bool, len(board))
for i := range visited {
visited[i] = make([]bool, len(board[0]))
}
wordSet := make(set)
prefixSet := make(set)
resSet := make(set)
for _, word := range words {
wordSet[word] = true
for i := 0; i < len(word); i++ {
prefixSet[string(word[:i+1])] = true
}
}
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
visited[i][j] = true
wordSearchIIDfs(board, visited, i, j, string(board[i][j]), wordSet, prefixSet, resSet)
visited[i][j] = false
}
}
res = make([]string, 0, len(resSet))
for k := range resSet {
res = append(res, k)
}
return res
}
func wordSearchIIDfs(board [][]byte, visited [][]bool, x int, y int, word string, wordSet set, prefixSet set, resSet set) {
if !prefixSet[word] {
return
}
if wordSet[word] {
resSet[word] = true
}
for i := 0; i < len(Directions); i++ {
adjX := x + Directions[i].x
adjY := y + Directions[i].y
if !inside(board, adjX, adjY) || visited[adjX][adjY] {
continue
}
visited[adjX][adjY] = true
wordSearchIIDfs(board, visited, adjX, adjY, word+string(board[adjX][adjY]), wordSet, prefixSet, resSet)
visited[adjX][adjY] = false
}
}
func inside(board [][]byte, x, y int) bool {
return x >= 0 && x < len(board) && y >= 0 && y < len(board[0])
}

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。